Shedding Light on Motion Episode 3: Relative Motion

The Shedding Light on Motion series is a visual treasure trove of demonstrations, animations, and explanations of all things motion! To an extent we’re all familiar with motion because we all move and we see movement everywhere, but a detailed knowledge of motion has allowed us to build the wonderful modern world that we live in.

In Episode 3, Relative Motion, we introduce students to the concept that the movement of an object is always relative to something else. We call it “sunrise” but is it really? Can we stand still and move around from place to place at the same time? If a car is moving forwards, can it also be moving backwards at the same time? And can we throw a single ball towards the left and towards the right at the same time? The answers to all these questions will be answered and along the way we will gain a much deeper understanding of velocity and acceleration!

The preview video below contains a 3-minute excerpt followed by a 1-minute trailer.

The Episode 3 Question Sheet for Students:
QS3 Relative Motion.
QS3 Relative Motion (extension questions).
Get the answers.

If you have ClickView, watch the whole episode here.
If you have Learn360, watch the whole episode here.
If you have Films on Demand, watch the whole episode here.
If you have Classroom Video, watch the whole episode here.
Most of our videos are also available on SAFARI Montage. Just log in and do a quick search.

Don’t have any of the above? Rent or buy the Shedding Light series and/or individual programs from our Vimeo page!!

The Transcript (which can be used as a textbook)

Contents:
Part A: Introduction. Whenever we talk about an object’s velocity, we’re really talking about its velocity relative to something else.
Part B: Relative Velocity. Two cars could be travelling next to each other at the same velocity, but relative to each other they are stationary. It’s a fairly simple concept but it has far-reaching effects on everything from rockets and space stations to movies and animations.
Part C: Frames of Reference. Sport is usually played on a stationary surface, but it can also be played on a moving surface as well. Just watch out for those fictitious forces!

Part A: Introduction

Two escalators, one working and one not working. I can walk slowly down the non-working one and approach the camera at about 0.5 m/s. However, when I walk slowly down the working one I don’t get any closer to the camera. I’m walking but I’m stationary. In this video, we’re going to look at the concept of relative motion, which has been essential in the development of spaceflight, airliners, and a whole lot of other things.

Right now, I’m not moving, and neither is the camera and neither are the trees behind me. And yet we know that the Earth is spinning so we must be moving.

The Earth does one complete rotation every 24 hours. Since the circumference of the Earth at the equator is about 40 000 km, anyone on the equator is moving at a speed of about 40 000 km /24 hours which equals nearly 1700 km/hr (1667km/hr) or 462 m/s. So in fact I am moving and so is everything else around me. But it gets even more complicated.

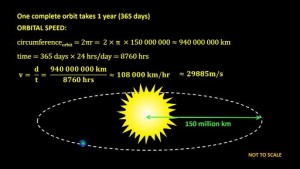The earth is travelling around the sun. One complete orbit takes one year. So what’s our orbital speed? Given that we travel in a more or less circular orbit about 150 million kilometres from the sun, the circumference of our orbit is about 940 million km (942,477,796 km). The time in hours is 365 days x 24 hours/day which equals 8760 hours. Our orbital speed is therefore about 108 000 km/hr (107589 km/hr) or just under 30 000 m/s (29885m/s).

Then we have the fact that the whole solar system is orbiting the whole galaxy at some huge speed (these NASA images are not showing our own galaxy by the way but galaxies that look very similar to our own) and of course our whole galaxy is also moving relative to other galaxies.

So why does it appear that nothing around me is moving. Well, since the ground, the trees, the camera and I are all travelling at the same speed, nothing that we can see is moving relative to anything else.

Standing next to these vehicles in this car park, it looks as if none of us are moving, but in fact we’re all moving at about 20 km/hr (relative to the water that is).

Whenever we talk about an object’s velocity, we really mean its velocity relative to something else. That something else is usually the Earth, but it doesn’t have to be.

Part B: Relative Velocity

These cars are both travelling at a velocity of 40 km/hr relative to the earth. However, the orange car, which is now being filmed from inside the black car, is not moving relative to the black car. It’s not getting further away and it’s not getting any closer. Relative to the black car, the velocity of the orange car is 0 km/hr.

If we film the two cars while they’re stationary relative to the earth, and ignore the trees and everything else, we can tell that the orange car isn’t moving because, once again, it’s not getting any closer and it’s not getting further away. If we play the 2 videos together, the orange car looks the same in both. The velocity of the orange car relative to the black car is zero in both situations.

Basically, the velocity of the orange car relative to the black car is the velocity of the orange car relative to the Earth minus the velocity of the black car relative to the Earth (V_OB = V_OE – V_BE).

Now here, relative to the earth, the black car is moving at 30 km/hr and the orange car is moving at 40 km/hr (relative to the ground). From inside the black car, the orange car can be seen passing the black car and then getting further and further away. Since it’s travelling 10 km/hr faster than the black car, 40 – 30 = 10, its speed relative to the black car is 10 km/hr.

Here the black car is stationary (relative to the Earth) and the orange car drives past at 10 km/hr (relative to the Earth). If we play both videos at the same time, we can see that from the perspective of the black car, where the camera is, the orange car looks the same in both. The orange car is travelling at 10 km/hr relative to the black car in both videos.

Now this time, relative to the earth, the black car is moving at 40 and the orange car is moving at only 30, 10 km/hr slower than the black car. 30 – 40 = -10 so the orange car’s velocity relative to the black car is therefore -10 km/hr. The negative sign tells us that the orange car is moving backwards relative to the black car.

Here the orange car is actually reversing with a velocity of 10 km/hr relative to the earth, or travelling at -10 km/hr if we define the direction that the cars are facing as positive. If I play both videos at the same time, we can see that from the perspective of the black car, the orange car looks the same in both. The velocity of the orange car relative to the black car is -10 km/hr in both situations, since we’ve defined the direction that the cars are facing as positive.

Hopefully you can now see why velocity is a far more useful concept that speed. Direction is important.

Let’s now look at a situation where the cars are travelling in opposite directions. We’ll define the black car’s direction as the positive direction. It’s travelling with a velocity of positive 20 but the orange car is travelling with a velocity of -30 km/hr. The difference in speed is only 30 – 20 or 10 km/hr, but the difference in velocity is negative 30 – 20 which equals -50 km/hr. The orange car’s velocity relative to the black car is -50 km/hr. To an observer in the black car, the orange car seems to be approaching at 50 km/hr. Here the orange car is approaching the stationary relative to the Earth black car at 50 travelling in the opposite direction so its velocity relative to the black car is also -50 km/hr. In both clips, the orange car looks pretty much the same, because even though it was travelling at different velocities relative to the Earth, it was travelling at the same velocity relative to the black car.

If the two cars are travelling at 40 km/hr in the same direction, then after one hour they will both have travelled 40 km. But, relative to each other they won’t have moved, and they’ll both be the same distance apart.

If the black car is travelling at 30 km/hr and the orange car is travelling at 40 km/hr, then after one hour the black car will have travelled 30 km and the orange car will have travelled 40 km. The orange car will be 10 km away from the black car. However, there’s another way of looking at it. Since the orange car is moving at 10 km/hr relative to the black car, then after one hour it will have moved 10 km away from the black car. All the mathematics fits!

Now when you’re quoting an object’s speed you don’t of course always have to say what its speed is relative to. If you say that a car is travelling at 60 km/hr it’s generally assumed that you’re talking about its speed relative to the Earth!

Here on this travellator, my speed relative to the camera is zero, because we’re both travelling at the same speed, but relative to the Earth, I’m moving at about 1 metre per second.

Skydiving footage often involves the camera person moving at the same velocity as the other skydivers. Everyone looks as if they’re just floating in the air, because their velocity relative to everyone else and to the camera is more or less zero. Relative to the ground though, they’re actually moving at about 200 km/hr.

Now this tiger is walking on this cat walk with a velocity of 1 m/s. If it walks at the same velocity on a platform which is moving at 2 m/s, then its velocity relative to the ground is the sum of the velocities: 3 m/s.

If we mark the position of each tiger at a given instant, wait a few seconds and then mark their positions again, we can see that the bottom tiger travelled three times further during the time interval because it was travelling three times faster.

If another tiger walks with a velocity of 1 m/s towards the left which we’ll define as -1 m/s, on a platform which has a velocity of 2 m/s towards the right, which we’ll define as +2 m/s, then its velocity relative to the Earth is 2 m/s + -1 m/s which is +1 m/s, or 1 m/s towards the right.

It’s fairly clear that the two tigers are travelling at the same velocity relative to the Earth.

If a boy now walks towards the rear of another platform with a velocity of -3m/s relative to the platform (blissfully unaware of the danger he’s in I might add), his velocity relative to the Earth is 2 + -3 m/s which equals -1 m/s, or 1 m/s to the left. I told you he was in danger.

(It’s the same formula as before but rearranged. If v_AB = v_AE – v_BE, then v_AE = v_AB + v_BE, where v_AB = the velocity of A relative to B and E stands for Earth)

The same mathematics applies to escalators. I can walk up this out-of-order escalator at about 0.5 m/s, or I can stand on the working escalator and travel with it at about 0.5 m/s, but if walk up the working escalator, then my speed relative to the Earth is 0.5 + 0.5 or 1 m/s.

Similarly, I can walk down the out-of-order escalator at about 0.5 m/s, but to reach the same speed, relative to the Earth that is, on the working escalator which is moving at 0.5 m/s upwards, I have to walk at 1 m/s downwards. Mathematically 0.5 m/s upwards + 1 m/s downwards = 0.5 m/s downwards. To put it another way, if we define upwards as positive then +0.5 m/s + -1 m/s = -0.5 m/s.

If I walk down the escalator at 0.5 m/s while it moves upwards at 0.5 m/s, my velocity relative to the Earth is 0.5 + -0.5 which equals zero.

If a plane is moving at 900 k’s an hr relative to the ground and I walk towards the front of the plane at 5 k’s an hr relative to the plane, I’m moving at 905 k’s an hr relative to the ground. When I walk to the back of the plane at 5 k’s an hour, I’m walking at only 895 k’s an hr relative to the ground.

Now I’ll just mention a slightly more high-end example. This wave is moving towards the shore, while I’m surfing along the wave towards the left. My direction therefore relative to the Earth is along a diagonal line, since the two yellow arrows add up to the green arrow.

Now the examples we’ve just looked at are fairly trivial, but understanding relative motion has been vital to the development of, for example, space travel and to the ability for two or more space craft to meet up in orbit and to dock. The guidance systems of aeroplanes rely on relative-velocity equations in their software all the time.

Commercial jets use ground-based radar signals and GPS signals from satellites to determine their location and their velocity relative to the Earth, but they also have small tubes called pitot tubes on their sides which measure the plane’s air speed, that is their speed relative to the air. All the information gets fed into a computer which tells the pilots and the autopilot what heading the plane should be on.

Ship captains also need to know their speed relative to the Earth and their speed relative to the water, so that they can navigate safely when for example they’re moving into a river port which has flowing water. You don’t want a 100,000 tonne ship crashing into a dock because it didn’t take into account the currents. A lot of Mathematics and Science goes into getting us from A to B safely!

Animators and special effects directors also have to understand relative motion. In this very simple animation, we immediately get the impression that the cars are moving towards the right, and they are… relative to the trees, but relative to the screen you’re watching, the cars aren’t moving at all.

I can set up a similar shot using real objects. I can film a moving shuttlecock with a moving camera on a moving trolley in front of a stationary background all relative to the Earth that is, or I can do the reverse and move only the background. So what’s happening here? It’s really hard to tell, but it turns out that the back ground is the one moving relative to the Earth. This scene looks very similar to the previous scene, but this time the shuttlecock was moving relative to the Earth. Of course the background and the shuttlecock are both moving relative to each other in both situations.

It’s a little like sunrise. We call sunrise “sunrise” because relative to the Earth, or from the perspective of the Earth, the sun is rising. However, relative to the sun or to an outside observer, the Earth is turning, and that’s what causes the sun to appear to rise every day. At sunset, the sun really does set relative to the Earth.

Part C: Frames of Reference

Closely related to the concept of relative velocity is the concept of the “Frame of Reference”. A Frame of Reference is a 3-dimensional space from which all your measurement of an object’s speed and position are made. The most common Frame of Reference is the Earth.

Here I’m throwing a ball upwards more or less vertically and it drops back down vertically. I can do the same thing on a trolley moving at a constant velocity. I think that I’m throwing the ball upwards vertically, but in fact because the trolley is moving, the ball leaves my hand travelling upwards and to the right (my left) so it follows a curved path. In the Earth’s Frame of Reference the ball is following a curved path. However, if we place the camera on the trolley, we can see that from the trolley’s frame of reference, I am still just throwing the ball vertically upwards. So is the ball moving up and down vertically or is it following a curved path. Well, the answer is that it’s doing both. It just depends on which frame of reference you make your measurements from.

A frame of reference travelling at a constant velocity, that is, at a constant speed and in the same direction, is called an inertial frame of reference. The word inertial comes from the word inert, which means unchanging or inactive.

Now even though the Earth is actually spinning, which means we are changing direction, it’s pretty much considered an inertial frame of reference. In any inertial frame of reference all the normal laws of Physics apply equally, even though we might think an object’s velocity is different in one frame of reference compared to another.

A ball being thrown back and forth between two people follows a curved path in the Earth’s frame of reference and the same applies if our frame of reference is slowly moving towards the right. It seems as if the ball is doing the same thing in both frames of reference.

However, if we film the moving ball on a moving trolley from the Earth’s frame of reference, how does the ball move? At first you might not notice a big difference. It looks like, as our eyes follow the trolley, two people are just throwing a ball back and forth. However, if turns out that in the Earth’s frame of reference, when I throw the ball towards screen left (what I think is forwards) it actually moves towards the right, because the trolley is moving faster towards the right than what I’m throwing it towards the left. Since my hand is moving backwards relative to the Earth faster than what I’m moving it forwards relative to the trolley, when I throw it, it initially moves upwards and to the right.

So is the ball moving towards the left when I throw it or towards the right? Well, once again, it’s doing both. It just depends on which inertial frame of reference you, as the observer, put yourself in. All the Laws of Physics still apply in both frames of reference.

However, what happens in an accelerating frame of reference? When the trolley is speeding up, the ball seems to get pushed to the side after it leaves my hand by a mysterious force acting in the opposite direction to my acceleration. If the trolley then decelerates, the ball seems to get pushed the other way. In an accelerating frame of reference, the normal Laws of Physics don’t seem to apply and what are called fictitious forces seem to appear.

Let’s look at it from the Earth’s frame of reference. As soon as the ball left my hand, I was obviously not applying any more force to it and it just followed a normal trajectory. However, the trolley and my hand, which were accelerating, kind of passed underneath where the ball should have landed from my point of view, and I ended up having to move my hand to my right, screen left, to catch it. It seemed to me as if there was an invisible force pushing it to my right.

When the trolley slowed down something similar happened. I threw the ball upwards, but because the trolley was moving to the right, the ball was projected upwards and to the right. The trolley suddenly slowed down but the ball kept going on its merry way and so it seemed, from the trolley’s frame of reference, to have been acted upon again by a sideways force.

In this aeroplane, which is taxiing at a constant velocity towards the runway, I’m throwing the ball vertically upwards, and everything seems normal in the plane’s inertial frame of reference. However, when the plane accelerates down the runway, the camera, the ball and I are in an accelerating frame of reference and a force seems to be pushing the ball backwards. However, if we could see the situation from outside the plane, I would be throwing the ball upwards and then accelerating towards it while it was in the air.

Once the plane reaches its cruising speed of about 800 km/hr, we’re back to an inertial frame of reference and everything seems normal again. If you’re in a plane, and you can’t see outside, there’s no real way of knowing you’re travelling at high speed, and you could play any sport you wanted, if you could find a plane big enough.

A simple back and forth game like tennis would look completely normal observed from inside the plane, but observed from the Earth we would see the ball moving faster one way than the other. You could even play sideways and everything would seem normal. The Laws of Physics are the same in any inertial frame of reference. It would be no different to playing sport on space ship Earth, because, remember, our whole Earth is always moving and so therefore is everything on it.

This is what we see from Earth when we watch two people playing tennis. But a Martian watching this game, with a very very powerful telescope, would see this, because the whole Earth is turning.

If this low-key back and forth throwing game was competitive, there would be no advantage to being at the front or at the back because in the trolley’s frame of reference, everything just seemed normal, despite the fact that from the Earth’s perspective the ball was going faster in one direction than in the other.

When the aeroplane and therefore our frame of reference decelerates on landing, fictitious forces once again appear.

It would be weird trying to play any kind of sport in a frame of reference which is not maintaining a constant velocity.

The study of reference frames and relative velocity played a key role in the formation of the theory of relativity by the famous German-born scientist Albert Einstein The theory of relativity is way too complicated for this video, but it led to a lot of new discoveries and inventions. For example, accurate GPS navigation, that is, using the signals sent by the GPS satellites to determine your location, relies on the theory of relativity. The theory also gave scientists a better understanding of how electrons move around atoms, which led to the development of the kinds of high-tech materials that are used in the latest computer chips.

We’ll take another look at reference frames when we study forces, because they can help explain things like why we supposedly get thrown forward in a car accident and why we supposedly fall backwards when a tram takes off suddenly.

Acceleration and velocity are two key concepts that form the basis of understanding motion. Formulas, tables, and videos are very important in the study of motion, but we can also use graphs to help us represent and describe an object’s motion. Graphing is a really powerful scientific tool when it comes to studying Motion and so it’s graphs that we’ll be looking at in our next episode. See you then.

CREDITS:

Written and directed by Spiro Liacos
Skydive-video-formationpractice-2013.ogv by Pigheart is licenced under Creative Commons Attribution-Share Alike 4.0 International.