Shedding Light on Motion Episode 4: Graphing Motion

In a 100-metre sprint, when do athletes reach their highest speed? When do they accelerate at the highest rate and at what point, if any, do they stop accelerating? In Episode 4 of the Shedding Light on Motion series, Graphing Motion, we look at how graphs can help us better understand the motion of athletes and of cars and other things.

The Shedding Light on Motion series is a visual treasure trove of demonstrations, animations, and explanations of all things motion! To an extent we’re all familiar with motion because we all move and we see movement everywhere, but a detailed knowledge of motion has allowed us to build the wonderful modern world that we live in.

The preview video below contains a 3.5-minute excerpt followed by a 1-minute trailer.

The Episode 4 Question Sheet for Students:
QS4 Graphing Motion.
Get the answers.

If you have ClickView, watch the whole episode here.
If you have Learn360, watch the whole episode here.
If you have Films on Demand, watch the whole episode here.
If you have Classroom Video, watch the whole episode here.
Most of our videos are also available on SAFARI Montage. Just log in and do a quick search.

Don’t have any of the above? Rent or buy the Shedding Light series and/or individual programs from our Vimeo page!!

The Transcript (which can be used as a textbook)

Contents:
Part A: Introduction. Graphs are used to display data in a way that helps us identify trends.
Part B: Distance vs Time Graphs. These graphs tell us where an object is at any given time and the information can, for example, help professional sprinters identify any weaknesses in their performance.
Part C: Velocity vs Time graphs. These graphs tell us how fast an object is moving at any given moment but they can also be used to calculate the distance an object has travelled and its acceleration!
Part D: Acceleration vs Time graphs. Sport is often not just about speed, it’s also about acceleration!

Part A: Introduction

In this episode of the Shedding Light on Motion series, we’re going to look at motion graphs. Graphs probably aren’t new to you; they’re used everywhere.
A table of information can be very useful, like this one showing how frequently letters are used, but graphs can show the information in a much clearer way. We can tell from the table that the letter “e” is the most commonly used letter, but the graph give us a visual representation that allow us to compare letter usage much more easily. Scientists and engineers use motion graphs to study and to analyse the way that things move.
Motion graphs give us lots of information about an object’s position, its velocity, and its acceleration. Let’s begin our study of motion graphs by taking a look at distance vs time graphs.

Part B: Distance vs Time Graphs

A distance vs time graph gives us information about where an object is at any given time. When, for example, sprinters are training for their big race, they don’t just record their times over the full 100 metres as is done in the race, they collect information about every stage of the sprint so that they can try to fix up any weaknesses.
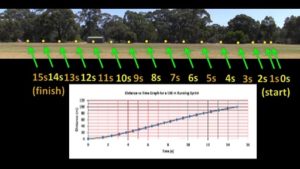I can run 100 m in about 15 s, so I’m clearly not much of a sprinter, but these are the times that were recorded at the 5 m mark, the 10 m mark and so on up to the 100 m mark. When you look at a table like this one, the amount of information can be overwhelming. However, we can use a distance vs time graph to get a simple picture of what happened during the sprint.
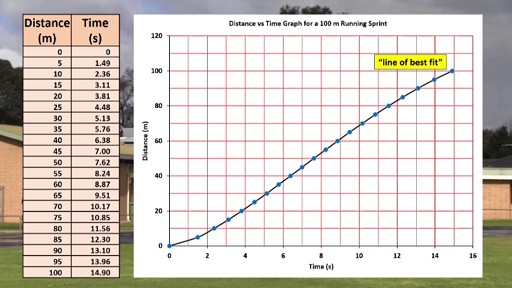A distance vs time graph shows distance on the y axis (in this case in metres) and time on the x axis (in this case in seconds). The first 5 metres took 1.49 seconds to complete, so we can put a dot at that point. I crossed the 10 metre mark after 2.36 seconds, so the next dot goes there. Repeating the procedure gives us a series of dots. We can then join the dots with what’s called a “line of best fit” which here takes the shape of a smooth curve. We can now get information from the graph. For example, how much distance did I cover in one second?
Let me zoom in a bit first. Reading off the graph, we can see that the answer is about 3 metres. After two seconds? After two seconds, I had covered about 8 metres, and after 3 seconds, I had covered about 14.2 metres. So in the first second of the sprint, between the gun going off and the 1-second mark, I travelled 3 metres, but in the second second, that is, between the 1 second mark and the 2-second mark, I travelled 8 – 3 metres, which is 5 m. In the third second, that is, between the 2-second mark and the 3-second mark, I travelled 14.2 – 8 metres, which is 6.2 metres.
So each second, I was covering more and more distance. And why is that? It’s because I was getting faster and faster, and by definition, a faster speed means that you cover more distance per second. My acceleration phase lasted about 5 or 6 seconds, after which I maintained a more or less constant speed for a few seconds. Towards the end I was slowing down. We’ll look at how you can tell I was slowing down shortly.
The orange line here is Jamaican athlete Usain Bolt’s distance vs time graph for his 2008 then world- record 100m sprint, which he completed in just 9.69 seconds. (He has since run the100m in just 9.58 seconds.) His graph is clearly much steeper than mine since he covered the same distance in much less time. Now we normally refer to the steepness of a graph as its gradient and in fact the gradient of a distance vs time graph gives a measure of an object’s speed.
Let’s look at a simple example. The two lines on this graph are displaying information about two cyclists that ride 400 m. Cyclist B covers the distance in 40 seconds, while Cyclist A covers the distance in only 25 seconds. Cyclist B’s speed is distance divided by time which equals 400 m / 40 seconds which equals 10 m/s. Cyclist A’s speed is 400 m / 25 seconds which equals 16 m/s.
Now the gradient of a line on a graph is equal to the rise over the run, that is, the change on the vertical y-axis divided by the change in the horizontal x-axis. So, Cyclist B’s gradient is the rise, which is 400 m, over the run, which is 40 seconds, which equals 10 m/s. Cyclist A’s gradient is 400 m / 25 seconds which equals 16 m/s. So I’ll say it again, the gradient of a distance vs time graph tells you the object’s speed. And it makes sense since speed = distance divided by time and the gradient equals the rise which is the distance over the run, which is the time.
We can now look at a slightly more advanced example. This is a distance vs time graph for a certain machine in a factory. The gradient of the line in Section A is a rise of 4 metres over a run of 4 seconds, which is 1 m/s. This was the speed of the machine. In Section B, the rise = 6 m, that is 10 m – 4 m, and the run is 2 s, that is 6 s – 4 s. The gradient of the line which is equal to the speed is 6 metres over 2 seconds, which is 3 m/s. So I’ll say it one more time: the gradient of a distance vs time graph tells you the object’s speed. Quite obviously, a higher gradient indicates a higher speed.
Now another useful thing to know is that on a distance vs time graph, a straight line indicates that the object is moving at a constant speed. In Section A, the machine moved 1 metre after 1 second, then another metre after another second and so on. In Section B, the machine moved 3 metres in 1 second and then another 3 metres the following second, that is, at a constant speed of 3 m/s.
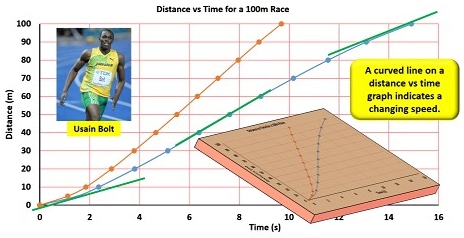A curved line on a distance vs time graph however, indicates a changing speed. At the start of my sprint, the gradient of the line is not very steep, because I was moving very slowly, but the line curves upwards meaning that its gradient is increasing, which means that my speed was increasing. Near the middle of the sprint, the gradient of the line is at its maximum because that’s where I reached my highest speed. Towards the end, the gradient becomes less and less steep because I was slowing down and covering less distance per second.
Usain Bolt’s line does the same thing, but obviously everything happens much more quickly. The curves are probably a little more obvious if we look at the graph from an oblique angle.
In a 100 m sprint the athletes run in a straight line, so distance vs time graphs are pretty straight forward. How do you draw a distance vs time graph though if the thing you’re studying is changing direction?
For example, in a 50 m pool, a 100m swimming race involves swimming to the end of the pool and then back again. So, if I swim 100 metres and record time data for every 10 metre split, I can use the data to draw up a distance vs time graph.
Now at the 50 m mark, I changed direction, but that isn’t indicated by this graph at all. How can I show that, for example, at the 70 mark, I was heading back towards the start and was in fact only 30 metres from it? Which also raises the question: at that point, had I travelled 70 m or only 30 m?
Well, we’re really talking about two different measurements: what we call distance and what we call displacement. We’re pretty familiar with the concept of distance: it’s how much ground you cover, or I suppose in this case the length of water you’ve swum through. Displacement is related to distance, but is a measure of how far you are from your starting position. Technically, the direction should also be quoted.
At the 70 m mark of my 100m swim, I had swum a distance of 70 m, but my displacement was 30 m towards the left, that is, I was 30 metres to the left of where I had started. Analysing displacement can tell us a lot. So instead of drawing a distance vs time graph, we can draw a displacement vs time graph.
This displacement vs time graph clearly indicates that at the 50 mark, I started swimming back towards the point I started from. After about 91 seconds, I reached the finish and my displacement was zero. In the first 50 m, the gradient of the line is positive, and so my velocity was positive, while in the second half of the swim, the gradient and therefore my velocity, were negative.
By the way, the fastest swimmers in the world swim nearly twice as fast as me. The 100m world record time for men is 46.91 seconds (César Cielo, Brazil) and for women is 52.06 seconds (Cate Campbell, Australia).
A displacement vs time graph is often referred to as a position vs time graph, because it shows where the object is in relation to its starting position. If I ask “what was my displacement at the 20 second mark?” it’s much the same as asking “what was my position at the 20s mark?”
Displacement vs time graphs are especially useful when scientists and engineers are designing machines which continuously repeat a movement, like the pistons in a car engine. Here, for example, the piston is moving upwards, while here it’s moving downwards.
Now whenever you draw a graph, the dots won’t necessarily all line up perfectly. These were the times recorded for a student who ran a 100 m sprint. When we draw up a displacement vs time graph, we see that the dots don’t really line up very well at all. If we connect each dot with a straight line, the graph makes it look as if the sprinter was travelling really fast here for example (since the gradient is high) but then slowed right down here (since the gradient is really low). Of course what really happened is that some of the times that were recorded just weren’t all that accurate. However, a “line of best fit” which best matches the overall trend of the dots, shows us a more accurate representation of the runner’s position at any given moment. If one dot is too high and the other one is too low, you just draw the line between them.
It’s not always easy to draw a line of best fit that’s curved, but you get better with practice. The line of best fit should average out all the errors.
Of course a line of best fit should quite often be a straight line. At this point something obviously went wrong, so it’s probably best to ignore this dot all together, and just draw in a straight line of best fit. Graphs and lines of best fit in fact make it obvious when errors have occurred.

Part C: Velocity vs Time graphs.

A velocity vs time graph as the name suggests provides information about an object’s velocity at any given moment. This velocity vs time graph shows Usain Bolt’s velocity during his 2008 100m then world-record sprint. At the beginning of the race, he wasn’t moving, but after 2 seconds, he reached a speed of about 8.9 m/s (32 km/hr), and after 4 seconds, he reached a speed of about 11.4 m/s. He reached his highest speed of 12.1 m/s at about the 6-second mark. As you can see, his velocity was changing a lot at the start, but it wasn’t changing as much as he neared his maximum velocity.
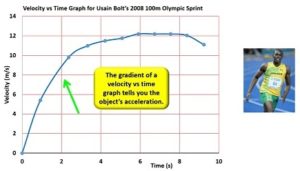
In fact, a velocity vs time graph doesn’t just indicate velocity. The gradient of the line tells you how quickly an object is changing its velocity. In other words, the gradient of a velocity vs time graph tells you the object’s acceleration. At the start Bolt was accelerating a lot, but as he got faster his acceleration eased off. He was still getting faster, but not as quickly. Eventually he reached his maximum speed. The gradient of the line here is zero and that tells us that his acceleration was zero; he was maintaining a constant speed. In contrast, this is my velocity vs time graph. As you can see, a much much lower top speed and a much much lower initial acceleration as well.
Now how does the introduction of a bike change things?
On the bike, my speed increased very slowly, but it kept increasing for a much longer amount of time, resulting in a higher speed by the end. Bikes are pretty amazing devices!
Let’s actually use a simple example to calculate an object’s acceleration, both by reading off the graph and by calculating the gradient of the line. What’s the acceleration of this object during Section A of its motion? It went from zero to 8 m/s in 4 seconds, so its acceleration, a = ?v/t which equals 2 m/s/s. But this also equals the gradient of the line which is a rise of 8 m/s over a run of 4 seconds, which is 2 m/s/s. In Section B of its motion it accelerated from 8 m/s to 12 m/s, a change of 4 m/s, in 4 seconds, so its acceleration was 1 m/s/s. But the gradient is also a rise of 4 m/s over a run of 4 seconds, which is 1 m/s/s. In Section C of its motion, it wasn’t changing its velocity at all, so its acceleration was 0 m/s/s, which is also the gradient of the line. In Section D, it slowed down from 12 m/s to 0 m/s, or in other words it changed its velocity by -12 m/s, in 4 seconds. Its acceleration was negative 3 m/s/s. Since the rise in this case is negative 12, the gradient is -12/4 or -3 m/s/s.
So I’ll say it again, the gradient of the line on a velocity vs time graph is equal to the object’s acceleration. Once again it makes sense because acceleration is the change in velocity over the change in time, and the gradient is the rise (which on this graph is the change in velocity) over the run (which on this graph is the time).
World-class sprinters can accelerate to about 9 m/s in about 2 seconds, so their average acceleration in the first 2 seconds is about 4.5 m/s/s.
A straight line on a velocity vs time graph indicates that the acceleration is constant: Here the object gained 2 m/s after 1 second, then another 2 m/s a second later, then another 2 m/s by the three-second mark and so on up to the 5-second mark. The object was gaining velocity at a constant rate.
A velocity vs time graph can also be used to calculate the displacement of an object. Here’s a simple velocity vs time graph of a car moving at 20 m/s for 10 s. How far does the car move in 10 seconds?
Well, if we start with our familiar average speed = distance / time equation and then transpose it to get distance = average speed x time, we can easily put in the values of speed and time and get 20 m/s x 10 s which equals 200 m.
However, it turns out that that the area under a velocity vs time graph, that is the area between the line and the x-axis, which is the area that’s flashing, tells us how far an object has moved. The area of the shaded rectangle is its height by its width which is 20 m/s times 10 s which equals 200 m. So I’ll say it again, the area under a velocity vs time graph tells you how far an object has moved from its starting position. Technically the area shows the displacement of the object, but in this case the displacement and the distance are the same (since the car is travelling in a straight line).
Let’s look at a more complex example. A car accelerates from 0 to 30 m/s (108 km/hr) in 20 seconds. Calculate how far it travels in that time. Well, how do you do that? We can still use our familiar equations but the average speed in this case is the average of 0 and 30 m/s which is 15 m/s. If something travels at an average speed of 15 m/s for 20 seconds, it must travel a distance of 15 m/s x 20 s which equals 300 m.
But let’s now look at the graph. I said a minute ago that the area under a velocity vs time graph tells you far the object has moved, that is its displacement. What’s the area of the shaded triangle which is what we call the area under the graph? Well, the area of a triangle is half base x height which equals half x 20 seconds x 30 m/s, which equals 300 m. The figures agree!
In this example the area under the graph in Part A is this shaded triangular region and, as we’ve just seen, we can use the formula Area = half base time height to calculate its area. The area under the graph in Section B is this shaded region which is the shape of what we call a trapezium. To calculate the area of this shaded region it’s probably easiest just to break it up into a triangle and a rectangle and then add the two areas together.
Now just for a minute let me explain the mathematics of units. Generally, when you have to calculate a quantity using a formula, whatever mathematical operation you perform on the numbers also has to be performed on the units.
So for example, what is my average speed if I swim 50 metres in 40 seconds? Speed = distance over time, so dividing 50 by 40 gives the number value, which is 1.25, but for a complete answer, I also have to divide the units as well. The unit for speed in this case is metres divided by seconds which we usually write as m slash s, though we pronounce this as metres per second.
Another example. What is the area of a basketball court? The area of a rectangle can be calculated using the formula area = length × width, which is 28 m × 15 m. The numerical answer of 28 x 15 is 420 but the units also have to be multiplied. Metres x metres is metres squared, although for area we commonly say square metres.
However in this example, we calculated the shaded area to be 300 m. The area in a graph is not in units of square metres or square cm or anything like that because graphs can represent any data. This graph has seconds as the unit on the x axis and m/s as the unit on the y-axis. To find the area of the shaded region, you still use the area = half base times height formula, but you have to multiply the numbers and the units. So what’s half x 20 seconds x 30 m/s? The number is 300 but what’s the unit? Well, s × m/s is the same as seconds x metres over seconds which equals metres. So the area is 300 metres. The area of a region of a graph depends on the units on the axes of the graph.
[NOT IN VIDEO: A shop is selling packs of 6 glasses for $4. What kind of value does this represent? If we go 6/4, we get 1.5. 1.5 what? Well, we also have to divide the units. 6 glasses / 4 dollars = 1.5 glasses/dollar. For every dollar that you spend you get 1.5 glasses.
If, on the other hand we go 4/6, we get 0.67. 0.67 what? 4 dollars / 6 glasses = 0.67 dollars/glass. Each glass costs 0.67 dollars.
Any time you perform a mathematical operation on number you have to perform the same operation on the units! Furthermore, the units actually give you useful information about what you have calculated.]
So just recapping, a velocity vs time graph, which, by the way is often called a v-t graph, written v-t but pronounced vt, displays information about an object’s velocity. This car for example started with a velocity of zero m/s and after 10 seconds was travelling at 15 m/s. The gradient of the line on a v-t graph equals the object’s acceleration, which here equals 30 m/s over 20 seconds which equals 1.5 m/s/s.
The area under the line of a v-t graph equals the displacement of the object, that is, how far the object has moved from its starting position, which as I said a minute ago is 300 m in this example.

Part D: Acceleration vs Time graphs.

Acceleration vs time graphs display, as the name suggests, an object’s acceleration at any given moment. This is Usain Bolt’s acceleration vs time graph, or a-t graph for his 2008 then world record sprint. I’ll place it next to his velocity vs time graph. At the start his speed increases rapidly and so the acceleration vs time graph shows this. Now in case you’re wondering about this gap here, we just don’t have enough data to say for certain what his initial acceleration was as he pushed off the block, but we would have to assume that it was probably higher than 6 m/s/s of course. As he got faster, he wasn’t accelerating as rapidly, and both graphs kind of level off. Between about the 6-second mark and the 8-second mark, he was travelling at more or less the same velocity, or in other words, he wasn’t accelerating at all, so the line on the acceleration graph shows a zero acceleration. At the end of the race, he started slowing down, that is he had a negative acceleration, and you can see that the line on the a-t graph dips below the axis into the negatives. Now even though the sprint lasted 9.69 seconds, the line stops here at about the 9-second mark because we don’t have enough data to say exactly what was happening in the last 5 metres or so. The same actually applies to the v-t graph as well.
Now the orange lines on these graphs show my acceleration and velocity in a 100m sprint. It’s fairly obvious looking at the a-t graph that I had a much smaller initial acceleration than Bolt, which corresponds to a lower gradient on the v-t graph. The a-t graph also shows that my acceleration went negative (in other words I started slowing down) at about the 7-second mark, which corresponds to a decrease in velocity of course on the v-t graph. Usain Bolt slowed down a lot in the final second of his race because he was so far ahead in 2008 that he started celebrating before he even crossed the finish line.
On the bike, depicted by the green lines, my acceleration was really low, but I was able to maintain it for a longer amount of time, resulting in a higher final speed. At no stage did I slow down over the 100m track. As I said, bikes are amazing machines. At about the 7-second mark, my legs were at about the limit of the speed at which they could peddle so I changed into a higher gear and continued to accelerate.
We can actually use a velocity vs time graph to draw up an acceleration vs time graph. Let’s do a simple example. In section A of this graph, the acceleration, which is equal to gradient of the line, is 8 m/s over 4 seconds, which equals 2 m/s/s. We can draw this onto our acceleration vs time graph like this. In Section B, the acceleration is 4 m/s over 4 seconds or 1 m/s/s. On the a-t graph we can draw in a horizontal line like this. In Section C, the object was maintaining a constant velocity. The gradient of the line is zero, which means that the acceleration is zero. The line on the a-t graph therefore has to run along the x-axis. In Section D, the object started slowing down, and came to a stop in 4 seconds. The acceleration is -3 m/s/s. The line on the a-t graph is therefore in the negative region.
We saw earlier how the area under a velocity vs time graph tells you how far the object has moved, or in other words how much the object has changed its position. In a similar kind of way, the area under an acceleration vs time graph tells you how much an object has changed its velocity.
The area under the line in Section A, that is the area between the line and the x-axis, is equal to the height by the width, which is 2 m/s/s times 4 seconds, which is 8 m/s. This was the change in velocity over the 4-second interval.
In section B, the area is 1 m/s/s times 4 seconds which is 4 m/s. Once again this was the change in velocity from the 4-second mark to the 8-second mark.
In Section C of the a-t graph the area is zero and this was also the change in velocity during Section C.
Finally, in Part D, the area bounded by the line and the x-axis is -3 m/s/s times 4 seconds which is -12 m/s. This once again was the velocity change as seen in the velocity vs time graph.
So I’ll say it one more time, the area under an acceleration vs time graph tells you how much an object has changed its velocity.
So that’s it for the basics of graphing motion. In our next episode we’re going to graphically examine the motion of objects that are in free fall. See you then.