Nuclear radiation can be incredibly dangerous, but it can also be incredibly useful to us. The Shedding Light on Nuclear Radiation series teaches students what nuclear radiation is and how humans have harnessed its awesome power.
In Shedding Light on Nuclear Radiation Episode 5: Half-Life and Activity, we examine how quickly radiation is given off by radiation-emitting substances. Some radioactive substances emit lots of radiation in a short amount of time while others emit radiation very slowly. These different rates of emission can be expressed in a quantitative way using the concepts of “half-life” and “activity”.
A 4-minute excerpt followed by a 1-minute trailer.
The Episode 5 Question Sheet for Students:
The PDF version.
Google The Google Doc version. Google
Get the answers.
If you have ClickView, watch the whole episode here.
If you have Learn360, watch the whole episode here.
If you have Classroom Video on Demand, watch the whole episode here.
If you have Access Video on Demand, watch the whole episode here.
You can also watch the episode on Safari Montage. (We can’t provide a link because each school has a different URL.)
Don’t have any of the above? Rent or buy the Shedding Light on Nuclear Radiation series (or individual programs) on Vimeo!!
Contents:
Part A: Introduction
Part B: Positrons
Part C: Positron Emission Tomography (PET Scans)
Transcript (more or less) (which also serves as a text book)
Part A: Introduction
Hi, everyone. In today’s lesson, we’re going to explore the really important concept of half-life. A radioactive substance’s half-life gives us a measure of how much time it will take for that substance to decay.
So, we’ve looked at quite a few nuclear decay modes already in our series. We’ve seen, for example, that uranium-238 is an alpha emitter, that carbon-14 is a beta-minus emitter, and that iodine-131 is a beta-minus and gamma emitter. When they emit nuclear radiation from their nuclei, they all turn into different atoms, since the number of protons in the nucleus changes.
However, if you start with say a trillion cobalt-60 atoms and a trillion iodine-131 atoms (not that I’m showing trillions here, but anyway) (both of which are beta and gamma emitters) and come back a week later, very few of the cobalt-60 atoms will have decayed, but about half of the iodine-131 atoms will have decayed.
Nuclear decay is a completely random process and you can never take a single unstable atom and know for sure when it’s going to decay. However, different radionuclides decay at different rates, rates which are measurable.
So, let’s look at this concept of half-life and at how it helps us better understand and use radioactive materials.
Part B: Half-Life, t1/2
We’ve seen how cobalt-60, a beta and gamma emitter, is used to sterilize medical and other equipment. When cobalt-60 atoms decay, they turn into nickel-60 atoms, which are stable. But, not every atom in a sample of cobalt-60 decays at the same time.
It turns out that if you start with a large number of cobalt-60 atoms, exactly half of them will decay in 5.27 years. Cobalt-60 has a half-life of 5.27 years. So, let’s say you start with 100 grams of cobalt-60. After 5.27 years, 1 half-life, half of the cobalt-60 atoms will have decayed and you will have only 50 grams of cobalt-60 left. Your sample will be made up of 50 grams of cobalt-60 and about 50 grams of nickel-60, which I’ve represented here as green dots. I should point out that cobalt-60 atoms and nickel-60 atoms have approximately the same mass, since they’re both made of 60 nucleons in total.
Neutrons and protons have approximately the same mass; there’s only about a 0.1 percent difference between them. An electron, by the way, has a mass of only about 1/2000 of the mass of a single proton or neutron.
So, as I said, after 1 half-life, what started as 100 grams of cobalt-60 is now 50 grams of cobalt-60, since half of the cobalt-60 atoms have decayed into nickel-60 atoms. After another 5.27 years (that is, 10.54 years later), half of the remaining cobalt-60 will decay so you’ll be left with only 25 grams of cobalt-60. Your sample will contain 25 grams of cobalt-60 and 75 grams of nickel-60. It’s tempting to think that if half have decayed after the first 5.27 years, the other half should decay in the next 5.27 years, but it doesn’t work that way. The number halves every half-life. After another half-life of 5.27 years (that is 3 half-lives or 15.81 years since the beginning) half of the cobalt-60 atoms you have left will decay again and you’ll be left with only 12.5 grams of cobalt-60. Your sample will contain 12.5 grams of cobalt-60 and 87.5 grams of nickel-60. The process will continue for a long time and the number of cobalt-60 atoms will just keep getting smaller. This also means that the radiation given off by the sample will slowly decrease.
Now in beta decay and gamma decay, the daughter nucleus and the parent nucleus have pretty much the same mass (as I said). However, that’s not the case with alpha decay. Alpha emitters lose 4 whole nucleons, so the mass of a sample of an alpha emitter decreases by a small but noticeable percentage as alpha particles are emitted. Now I didn’t want to make a big deal of it, but I just thought I’d mention it.
The half-lives of different substances vary from tiny fractions of a second to billions of years. This table shows a few examples. By the way, the symbol used for half-life is t1/2.
As you can see, uranium-238 has a very long half-life, so a sample of it gives off very few alpha particles and gamma rays per second and it lasts a long time. Fluorine-18, though, has a very short half-life. The atoms are very unstable and so lots of decays occur per second. Notice how there is a huge difference in the half-lives of plutonium-239 and -238. A difference of just one neutron can change the stability of an atom in a big way. When it comes to half-life, it turns out that there are no obvious patterns in the proton to neutron ratio that allow us to predict what the half-life of a natural radioisotope would be. It can only be determined experimentally.
Lots of things in nature do follow certain patterns; electrons in electron shells for example fill up in a more or less logical manner, 2,1; 2,2; 2,3; and so on, but, there is no pattern when it comes to half-lives. They vary widely even if there isn’t much difference in the numbers of protons or neutrons. However, beta-plus emitters always have fairly short half-lives.
It also turns out that the half-life of a radionuclide is not affected by anything. Heating it doesn’t make a difference and neither does burning it or cooling or chemically reacting with anything.
So, let’s do a question? How much time will it take for 20 grams of radioactive iodine-131 to get down to only 2.5 grams?
Well, 20 grams gets down to 10 grams in 1 half-life, down to 5 grams after another half-life and down to 2.5 grams after another half-life. 20g ? 10g ? 5g ? 2.5g
So, that’s three half-lives and each one is 8 days, so 3 x 8 = 24 days. Mathematically it’s not difficult to calculate, as long as you remember the concept that half of the atoms of a radioisotope will decay in one half-life.
Radioactive tracers used in nuclear medicine generally have short half-lives. A radionuclide is introduced into the body, it emits whatever radiation is required and within a short time it has completely changed into a stable isotope of another element.
In Episode 2 of our program, we saw how space probes that explore the far reaches of the solar system like Voyager 2 and New Horizons use radioisotope thermoelectric generators (or RTG’s) to provide electricity for their electrical systems. Voyager 2 flew past Jupiter, Saturn, Neptune and Uranus, while New Horizons flew past Jupiter and Pluto. Both space probes are still travelling away from the sun at about 15 or so kilometres per second. The RTG’s powering the electrical systems of the space probes use plutonium-238 as a heat source to generate electricity. Plutonium-238 is an alpha emitter and it generates heat as it decays into uranium-234. Its half-life is 87.7 years. When Voyager 2 was launched in 1977, the 3 onboard RTGs were generating about 160 Watts of electrical power in total. This power production has been decreasing ever since and will halve by the year 2065. However, it’s expected that there won’t be enough power to power any of its onboard systems by about 2030. It’s been a remarkably long and successful mission, made possible by plutonium-238.
So, radioactive substances just randomly give off nuclear radiation. Generally, the shorter the half-life, the more nuclear radiation is given off per second. But what kind of numbers are we talking about?
For example, cobalt-60 is a beta and gamma emitter. How many beta particles and gamma rays are produced in a given sample of cobalt-60 per second? Let’s take a look.
Part C: Activity (in Becquerels)
A radionuclide with a longer half-life does not produce as much nuclear radiation per second as a radionuclide with a shorter half-life, assuming you’ve got the same number of atoms in your sample of course.
The number of decays that occur per second in a sample of radioactive material is called the sample’s “activity”. The unit for activity is the becquerel, Bq (named after Henri Becquerel, the discoverer of radioactivity).
An activity of 1 becquerel = 1 decay per second.
This table gives some examples of the activities of various radionuclides in becquerels per gram of the material.
In general, a higher activity results in a shorter half-life. If we look at the first two examples in the table, which have really long half-lives, their activity per gram is measured in the thousands of becquerels. However, if the half-life is measured in years, days or hours, we can see that the activity is measured in billions (10 to the 9 is a 1 followed by 9 zeros, that is, a billion), thousands of billions, millions of billions, and billions of billions of decays per second. In a gram of U-238, which actually consists of about 2.5 x 1021 atoms there are only 12,500 decays (alpha decays) per second. 12,500 is basically zero compared to 2.5 x 1021 so it takes a long long time before they’ve all decayed, and that’s an understatement. Of course, the activity of a sample of a radionuclide depends on its half-life AND on how many atoms are in the sample.
| Radionuclide | Uses | Decay Mode | Half-life (T1/2) | Activity
(Bq per gram) |
| U-238 | naturally occurring |  ,  |
4.5 billion years | 12,500 |
| K-40 | naturally occurring |  –, |
1.25 billion years | 262,700 |
| U-235 | naturally occurring, nuclear fuel | , |
704 million years | 81,000 |
| Am-241 | smoke detectors | , |
432 years | 126 x 109 |
| Sr-90 | heat source for space probes | – |
28.8 years | 5.2 x 1012 |
| Co-60 | cancer therapy | –, |
5.27 years | 44 x 1012 |
| P-32 | DNA research | – |
14.4 days | 1015 |
| I-131 | medical diagnostics and therapy | –, |
8.02 days | 4.6 x 1015 |
| F-18 | PET scans | + |
1.83 hours (110 minutes) | 3.5 x 1018 |
The activity of an actual sample can be determined by a simple relationship:
Activity = activity per gram x the number of grams.
For example, the activity of 2 grams of U-235 = 81,000 Bq/g (the figure in the table) x 2 g = 162,000 Bq, that is, 162,000 decays per second.
Over time, as a radionuclide decays, its activity decreases.
Let’s look at an example using cobalt-60, which has a half-life of 5.27 years and an activity of 44 x 1012 Bq/gram. If, for example, a hospital acquires a sample of 3 grams of cobalt-60 to use in radiation therapy, the activity of the sample will be, let’s use the formula, 44 x 1012 Bq/gram x 3 g = 132 x 1012 becquerels. Let me put the information into a table. Now, after 1 half-life (5.27 years), half of the cobalt-60 atoms will have decayed into nickel-60 atoms, so the remaining 1.5 grams of cobalt-60 atoms will produce an activity of only 66 x 1012 becquerels. This is, of course, half of what it had originally. After 2 half-lives, the activity of the sample will reduce by half again to 33 x 1012 becquerels. Now this general pattern holds for all radioactive substances that decay into stable atoms. Nickel-60 is stable, so the only radiation being emitted is coming entirely from the cobalt-60.
If, however, the initial sample decays into a nuclide that is also radioactive, then the activity will not necessarily decrease by half, since the daughter nucleus will also emit radiation, and the mathematics gets a little more complicated. We’re going to keep it simple though.
For example, strontium-90 decays by beta-minus emission into yttrium-90 with a half-life of 28.8 years. However, yttrium-90 is also radioactive. It decays, also by beta-minus emission, into zirconium-90 with a half-life of 64.1 hours. Zirconium-90 is stable. So, after 1 half-life, half of the strontium-90 atoms will have decayed, but the activity of the sample will not have halved because there will be a whole bunch of yttrium-90 atoms in it that are also giving off radiation.
Now to express these large numbers, scientists often use prefixes on the units. So, for example, 1,000 becquerels can be written as 1 kilobecquerel or 1 kBq. k stands for kilo which means a thousand, just like the word kilometre, which means a thousand metres. One million becquerels can be written as 1 megabecquerel. The capital M stands for mega; 1 million. Next, we can write 1 billion becquerels as 1 gigabecquerel, G for giga which is a billion, 1 trillion becquerels as 1 terabecquerel, T for tera which is a trillion, 1 quadrillion becquerels as 1 petabecquerel, P for peta which is a quadrillion, and finally 1 quintillion becquerels as 1 exabecquerel, E for exa which is 1 quintillion, which a 1 followed by 18 zeros. There’s always big numbers involved when you’re talking about atoms!!
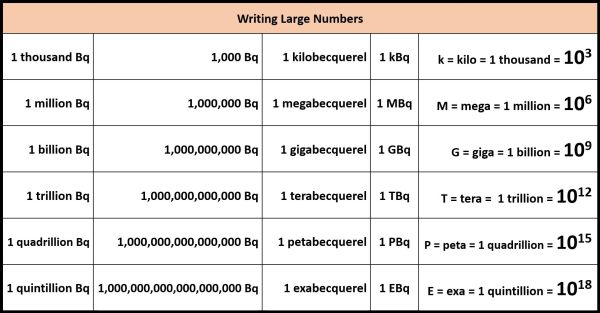So, if we go back to this table, I can add another column and re-write these values. 12,500 Bq can be written as 12.5 kBq, since there are 1000 Bq in a kilobecquerel. 81,000 Bq can be written as 81 kBq. This one can be written in gigabecquerels since 109 is giga, these two in terabecquerels 1012 is tera, these two in petabecquerels (1015), and this one in exabecquerels. As I said, big numbers!
Now our understanding of half-lives and activity has allowed us to work out the age of certain rocks which has allowed us to work out the approximate age of the Earth.
It’s also allowed us to work out how old various ancient artefacts are. How so? Well, that’s what we’ll be looking at in our next episode. See you then.
CREDITS:
Written and directed by Spiro Liacos
“How radiopharmaceuticals help diagnose cancer and cardiovascular disease” by IAEAvideo. https://youtu.be/mQjCTTKWOFU. Creative Commons License.
Footage of Gamma Irradiation © BGS Beta-Gamma-Service. Used with Permission. See “BGS Beta-Gamma-Service _ Using gamma rays to destroy germs_ How radiation sterilization works” by BGS Beta Gamma Service. https://youtu.be/hblMTH09KJQ
Special thanks to the Museum of Cycladic Art, Athens, Greece. https://cycladic.gr/en
Special thanks to the people of Papingo, Epirus, Greece.
Special thanks to the University of Melbourne School of Physics.